i
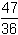 × 324 =423.
× 324 =423.LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA KONKURSOWE Z ETAPU I
DLA KLAS II GIMNAZJUM
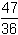 liczby zapisanej tymi samymi cyframi co szukana liczba tylko w porządku odwrotnym.
liczby zapisanej tymi samymi cyframi co szukana liczba tylko w porządku odwrotnym.
x - szukana liczba
400 < x < 500
Z informacji, że suma cyfr tej liczby x dzieli się przez 9 wynika, że sama liczbax dzieli się przez 9.
Niech y oznacza liczbę zapisaną tymi samymi cyframi co x, tylko w odwrotnym porządku. Z informacji, że x =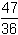 ×y
wynika, że że y =
×y
wynika, że że y = 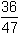 ×x, a więc:
×x, a więc:
x dzieli się przez 47.
Najmnieszą liczbą która dzieli się przez 9 i 46 jest 9 × 46 = 423.Sprawdzenie:
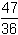 × 324 =423.
× 324 =423.Paweł Sobierajski