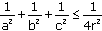
LIGA ZADANIOWA UMK W TORUNIU 2001/2002
ZADANIA Z PREZENTU WAKACYJNEGO

Zadanie 11

Niech a, b, c i r oznaczają długości boków i promień okręgu wpisanego w trójkąt. Wykaż, że:

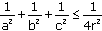
Dowód

Narysowane promienie dzielą boki na odcinki:

a=x+y   b=y+z   c=z+x

Połowa obwodu trójkąta wynosi

p=x+y+z.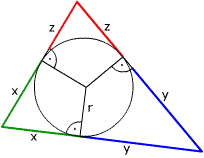

Ze wzoru Herona na pole S trójkąta 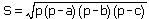wynika, że

. Z drugiej strony S=r(x+y+z). Wynika stąd, że

r(x+y+z)=

r2(x+y+z)2=(x+y+z)xyz

Pokażę, że (x+y)2 ł 4xy  dla dowolnych liczb x, y.

Dowód: (x+y)2 - 4xy = (x-y)2 ł 0. Koniec dowodu.

Mamy więc:

(x+y)2 ł 4xy
(y+z)2 ł 4yz
(z+x)2 ł 4zx.


Ostatecznie otrzymujemy, że:

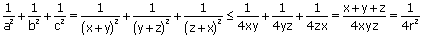
Jakub Gierszał