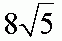
LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA PRZYGOTOWAWCZE DO ETAPU III 
DLA KLAS II GIMNAZJUM

Zadanie 3

Niech punkt (0;0) będzie środkiem kwadratu, a punkt (1;3) niech będzie jednym z jego wierzchołków. Wyznaczyć pozostałe wierzchołki tego kwadratu i obliczyć pole i obwód tego kwadratu

Rozwiązanie

Aby narysować punkt(1;3) należy od punktu (0;0) przesunąć się o 3 jednostki w górę i 1 jednostkę w prawo

Aby otrzymać punkt będący przeciwnym wierzchołkiem kwadratu należy posunąć się z punktu (0;0) o 3 jednostki w dół i 1 jednostkę w lewo.

Wiadomo, że przekątne w kwadracie przecinają się pod kątem prostym. Skoro, aby wyznaczyć wierzchołek (1;3) przesunęliśmy się z punktu (0;0) o 3 jednostki w górę i 1 jednostkę w prawo, to aby wyznaczyć kolejny wierzchołek należy przesunąć się z punktu (0;0) o 1 jednostkę w górę i 3 jednostki w lewo. (Wtedy tylko, będzie spełniony warunek kąta prostego)

Aby otrzymać punkt będący przeciwnym wierzchołkiem kwadratu niż punkt (-3;1) należy posunąć się o 1 jednostkę w dół i 3 jednostki w prawo.

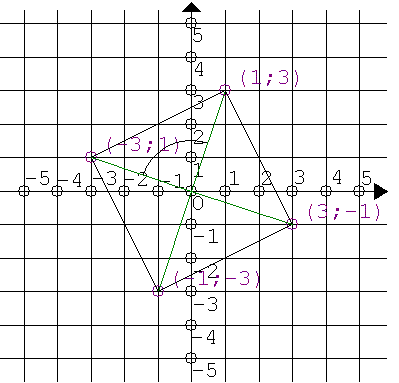
Wszystkie otrzymane punkty łączymy ze sobą odcinkami i w ten sposób powstaje następujący kwadrat:

Zauważmy, że można narysować w tym kwadracie trójkąt prostokątny, którego znamy 2 boki.

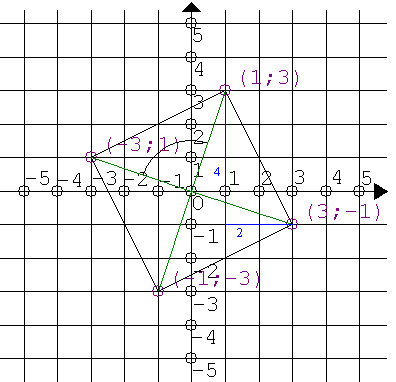
Z twierdzenia Pitagorasa obliczamy długość boku kwadratu (x)):

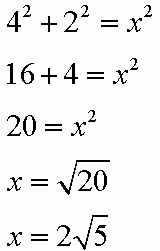
Pole tego kwadratu wynosi:

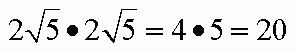
Obwód tego kwadratu wynosi:

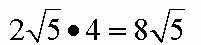
Odpowiedź

Pole otrzymanego kwadratu wynosi 20, a obwód