LIGA ZADANIOWA UMK W TORUNIU 2002/2003
PREZENT WAKACYJNY
DLA UCZNIÓW GIMNAZJUM
Zadanie 5
Rozwiązać w liczbach naturalnych równanie:
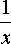 +
+
 =
=
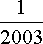 .
.
Rozwiązanie:
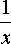 +
+
 =
=
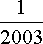
Jak widać musi być spełniony następujący warunek:
x, y > 0
ponieważ mają to być liczby naturalne i nie można dzielić przez 0. (!)
Doprowadźmy ułamki po lewej stronie do wspólnego mianownika:
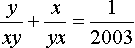 / × xy
/ × xy
x + y = 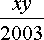 /
/  2003
2003
2003(x+y) = xy / - 2003(x+y)
xy-2003(x+y) = 0
xy-2003x-2003y = 0 / + 2003 × 2003
xy-2003x-2003y+2003 × 2003 = 2003 × 2003
x(y-2003)-2003(y-2003) = 2003 × 2003
(y-2003)(x-2003) = 2003 × 2003
2003 jest liczbą pierwszą, a więc mogą być tylko 3 możliwości:
- y-2003 = 2003 i x-2003 = 2003
y = 4006 i x = 4006
- y-2003 = 1 i x-2003 = 2003 × 2003
y = 2004 i x = 2003 + 20032
- y-2003 = 2003 × 2003 i x-2003 = 1
y = 2003 + 20032 i x = 2004
Mateusz Grupa
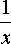 +
+
 =
=
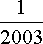 .
.
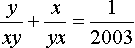 / × xy
/ × xy
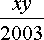 /
/