|
LIGA ZADANIOWA UMK W TORUNIU
ZADANIA W ROKU SZKOLNYM 2002/2003
Prezent wakacyjny dla uczniów gimnazjum 
|
| Zadanie 1 |
Na ile sposobów liczbę 2003 można przedstawić w postaci różnicy kwadratów dwóch liczb naturalnych?
|
| Zadanie 2 |
Oblicz:
 , ,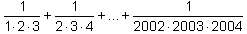 . .
|
Rozwiązanie Kamila Brożyny
|
| Zadanie 3 |
Niech s(n) oznacza sumę cyfr liczby naturalnej n. Czy istnieje liczba naturalna n, dla której zachodzi równość:
-
n + s(n) + s(s(n)) = 2003
-
n + s(n) + s(s(n)) +s(s(s(n)))= 2003
|
Rozwiązanie Magdy Ekert
|
| Zadanie 4 |
|
Napisać pięć następnych liczb zgodnie z wyznaczoną regułą: 1, 11, 21, 1112, 3112, 211213, 312213, 212223, ...
|
| Zadanie 5 |
Rozwiązać w liczbach naturalnych równanie  . .
|
Rozwiązanie Mateusza Grupy
|
| Zadanie 6 |
Rozwiązać w liczbach naturalnych równanie x + y + z = x×y×z.
|
Rozwiązanie Michała Kęder
|
| Zadanie 7 |
Rozwiązać równanie: 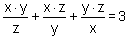
- w liczbach naturalnych,
- w liczbach całkowitych.
|
Rozwiązanie Marcina Kopczyńskiego
|
| Zadanie 8 |
Wyznaczyć wszystkie liczby sześciocyfrowe, które zwiększą się sześciokrotnie, gdy ich trzy ostatnie cyfry przeniesiemy bez zmiany porządku na początek.
|
Rozwiązanie Agaty Kozińskiej
|
| Zadanie 9 |
Wyznaczyć wszystkie liczby, których pierwszą cyfrą jest dwójka i które po przeniesieniu dwójki na koniec zmniejszą się dwa razy.
|
| Zadanie 10 |
Pierwszą cyfrą pewnej liczby jest 7. Cyfrę tę przeniesiono na koniec i wówczas otrzymano liczbę dwukrotnie mniejszą. Co to za liczba?
|
Rozwiązanie Macieja Lewandowskiego
|
| Zadanie 11 |
Wyznaczyć wszystkie liczby naturalne n tak, aby liczba  była liczbą całkowitą. była liczbą całkowitą.
|
Rozwiązanie Iwony Lis
|
| Zadanie 12 |
Wyznaczyć wszystkie możliwe czwórki liczb naturalnych o następującej własności: iloczyn dowolnych trzech z nich powiększony o jeden jest podzielny przez czwartą z nich.
|
Rozwiązanie Mateusza Mickiewicza
|
| Zadanie 13 |
Na płaszczyźnie dane są trzy punkty nie leżące na jednej prostej. Ile istnieje równoległoboków, których trzy wierzchołki pokrywają się z danymi punktami?
|
Rozwiązanie Magdy Nieżurawskiej
|
| Zadanie 14 |
W przestrzeni dane są cztery punkty nie leżące na jednej płaszczyźnie. Ile istnieje równoległościanów, których cztery wierzchołki pokrywają się z danymi punktami?
|
Rozwiązanie Marcina Pezdy
|
| Zadanie 15 |
Opisać konstrukcję prostej, która dzieli dany trójkąt na dwa wielokąty o równych polach.
|
| Zadanie 16 |
Opisać konstrukcję prostej, która dzieli dany czworokąt na dwa wielokąty o równych polach.
|
| Zadanie 17 |
Wewnątrz czworokąta wypukłego znaleźć punkt, którego suma odległości od wierzchołków jest najmniejsza.
|
Rozwiązanie Artura Rasztubowicza
|
| Zadanie 18 |
Dany jest trójkąt prostokątny ABC. Dla punktu X leżącego na przeciwprostokątnej AB niech M i N będą takimi punktami leżącymi na przyprostokątnych AC i BC odpowiednio, że XM ^ AC i XN ^ BC. Przy jakim położeniu punktu M
- odcinek MN jest najkrótszy?
- pole prostokąta XMCN jest największe?
|
Rozwiązanie Magdy Ryczkowskiej
|
| Zadanie 19 |
W trójkącie ABC poprowadzono dwusieczną AD. Wyznaczyć miary kątów trójkąta ABC jeśli środek okręgu wpisanego w trójkąt ABD jest jednocześnie środkiem okręgu opisanego na trójkącie ABC.
|
Rozwiązanie Pawła Rzymyszkiewicza
|
| Zadanie 20 |
W trójkącie ABC poprowadzono z wierzchołka C wysokość i środkową. Podzieliły one kąt wewnętrzny przy wierzchołku C na trzy równe kąty. Wyznaczyć kąty trójkąta ABC.
|

 ,
,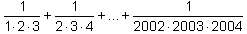 .
. .
.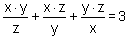
 była liczbą całkowitą.
była liczbą całkowitą.