LIGA ZADANIOWA UMK W TORUNIU 2002/2003
PREZENT WAKACYJNY
DLA UCZNIÓW GIMNAZJUM

Zadanie 7

1. w liczbach naturalnych,
2. w liczbach całkowitych.

Rozwiązanie

---

1. Możemy rozwiązać to równanie korzystając z nierówności Cauchy'ego, która mówi, że:

   Średnia arytmetyczna liczb nieujemnych jest większa lub równa średniej geometrycznej tych liczb.

   

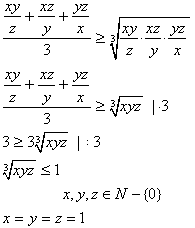
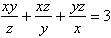   Odpowiedź: Jedynym rozwiązaniem równania    w liczbach naturalnych jest trójka liczb: x = 1, y = 1, z = 1.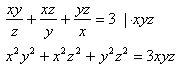
   
   

   ---

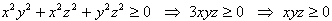
2. Pomnóżmy obie strony równania przez iloczyn mianowników:

   

   Suma iloczynów kwadratów nie może być mniejsza od 0:

   

   Ponieważ nie wolno dzielić przez 0, żadna z niewiadomych x, y, z nie może być równa 0, więc na pewno:

   xyz > 0

   Teraz również tu możemy zastosować nierówność Cauchy'ego: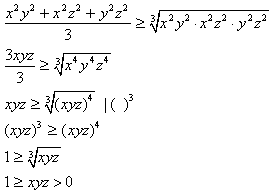

   

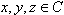   Wiedząc dodatkowo, że   i, że 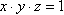mamy 4 możliwości:

   Możliwość	x	y	z
   1.	1	1	1
   2.	1	-1	-1
   3.	-1	1	-1
   4.	-1	-1	1

   Odpowiedź: Rozwiązaniami równania
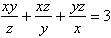
   w liczbach całkowitych są cztery trójki liczb:

   x	y	z
   1	1	1
   1	-1	-1
   -1	1	-1
   -1	-1	1

Marcin Kopczyński