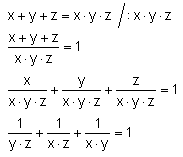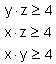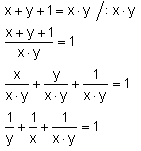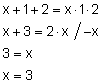LIGA ZADANIOWA UMK W TORUNIU 2002/2003
PREZENT WAKACYJNY
DLA UCZNIÓW GIMNAZJUM
Zadanie 6
Rozwiązać w liczbach naturalnych równanie x + y + z = x×y×z.
Rozwiązanie
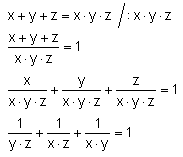
Widzimy, że żadna z par liczb yz, xz i xy nie może być równa 1, ponieważ wynik byłby większy od 1.
ZAŁOŻENIE I
Załóżmy, że żadna z liczb nie jest równa 1.
Wtedy najmniejszą możliwą liczbą do podstawienia byłaby dwójka i prawdziwe byłoby twierdzenie:
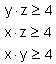
Wiemy, że im większy mianownik w ułamku o liczniku 1, tym mniejsza liczba.
Opierając się o początkowe obliczenie, widzimy, że to założenie nie ma sensu, gdyż najmniejszym mianownikiem byłoby 4, a wtedy:
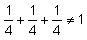
Z tego wynika, że jedną z liczb musi być 1. Do dalszych obliczeń załóżmy, że jest to z.
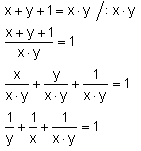
Oczywiście gdy x,y>1.
ZAŁOŻENIE II
Załóżmy, że ani x ani y nie jest równe 2 i oczywiście jest większe od 1.
Wtedy najmniejszą możliwą liczbą do podstawienia byłaby trójka i prawdziwe byłoby twierdzenie:
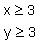
Opierając się o poprzednie obliczenie, widzimy, że to założenie nie ma sensu, gdyż najmniejszym mianownikiem byłoby 3, a wtedy:
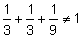
Z tego wynika, że drugą z liczb musi być 2. Do kolejnego obliczenia załóżmy, że jest to y.
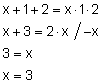
Odpowiedź
Rozwiązaniem są liczby 1, 2 i 3.
Michał Kęder