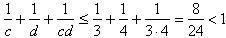LIGA ZADANIOWA UMK W TORUNIU 2002/2003
PREZENT WAKACYJNY
DLA UCZNIÓW GIMNAZJUM
Zadanie 12
Wyznaczyć wszystkie możliwe czwórki liczb naturalnych o następującej własności: iloczyn dowolnych trzech z nich powiększony o jeden jest podzielny przez czwartą z nich.
Rozwiązanie
Niech a, b, c, d, gdzie a Ł b Ł c Ł d, oznacza czwórkę liczb naturalnych o podanej własności.
Wówczas liczby:
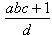 ,
, 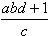 ,
, 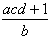 ,
, 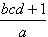
są naturalne, a więc ich iloczyn jest też liczbą naturalną.
Po przemnożeniu tych liczb otrzymujemy wynik:
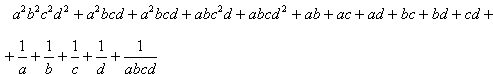
Wynika stąd, że liczba 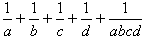 musi być naturalna.
musi być naturalna.
Zauważmy jeszcze, że największym wspólnym dzielnikiem dowolnych dwóch liczb spośród a, b, c, d jest 1.
Dla przykładu pokażę, że NWD(a,d)=1.
Niech 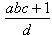 = k.
Wtedy abc + 1 = kd, więc kd - abc = 1. = k.
Wtedy abc + 1 = kd, więc kd - abc = 1.
Jeśli więc jakaś liczba naturalna n jest wspólnym dzielnikiem liczb a i d, to liczba kd - abc też dzieli się przez n czyli 1 dzieli się przez n. Jedynym naturalnym dzielnikiem liczby 1 jest 1, więc n = 1. |
Zadanie sprowadza się więc do wskazania liczba naturalnych a, b, c, d takich, że:
-
a Ł b Ł c Ł d;
- NWD(a,b) = NWD(a,c) = NWD(a,d) = NWD(b,c) = NWD(b,d) = NWD(c,d) = 1;
- Liczba
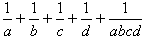 jest naturalna.
jest naturalna.
- Pokażę, że a < 3.
Gdyby a ł 3, to ze względu na własność II, wszystkie liczby a, b, c, d musiałyby być parami różne, więc mielibyśmy, że
a ł 3,
b ł 4,
c ł 5,
d ł 6.
Wtedy jednak 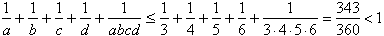
.
- Pokażę, że a ą 2.
Gdyby a = 2, to ze względu na własność II, wszystkie liczby a, b, c, d musiałyby być parami różne, i liczby b, c, d musiałyby być nieparzyste, więc mielibyśmy, że
a = 2,
b ł 3,
c ł 5,
d ł 7.
Wtedy
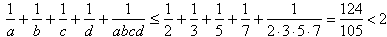
Więc jedyną możliwością byłoby, że:
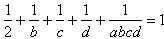 ,
,
stąd:
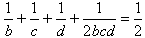 ,
,
ale 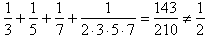 ,
,
a już 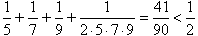 .
.
- Wiemy już więc, że a = 1.
Zatem liczba 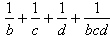 musi być naturalna.
musi być naturalna.
- Pokażę, że b = 1.
Jeśli b ł 2, to
- dla b = 2, c = 3, d = 5 mamy:
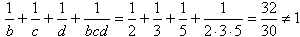
- dla b = 2, c ł 5, d ł 7 mamy:
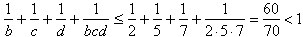
- dla b ł 3, c ł 4, d ł 5 mamy:
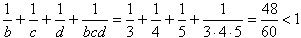
- Teraz wiadomo już, że a = 1 i b = 1.
Zatem liczba 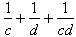 musi być naturalna.
musi być naturalna.
- Dla c = 1 mamy:
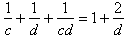 ,
,
więc d = 1 lub d = 2.
- Dla c = 2 mamy:
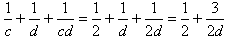 ,
,
więc d = 3.
- Dla c ł 3 mamy:
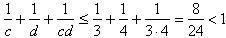
a więc więcej rozwiązań już nie ma.
Odpowiedź:
Jedyne rozwiązania to:
- 1, 1, 1, 1;
- 1, 1, 1, 2;
- 1, 1, 2, 3.
Mateusz Mickiewicz
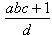 ,
, 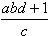 ,
, 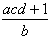 ,
, 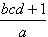
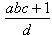 ,
, 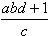 ,
, 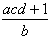 ,
, 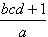
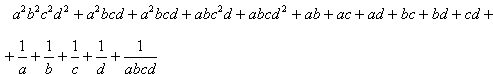
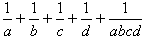 musi być naturalna.
musi być naturalna.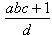 = k.
Wtedy abc + 1 = kd, więc kd - abc = 1.
= k.
Wtedy abc + 1 = kd, więc kd - abc = 1.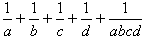 jest naturalna.
jest naturalna.
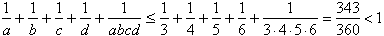
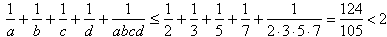
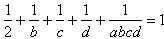 ,
,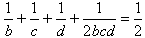 ,
,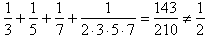 ,
,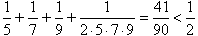 .
.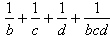 musi być naturalna.
musi być naturalna.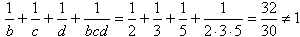
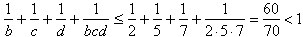
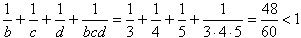
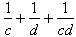 musi być naturalna.
musi być naturalna.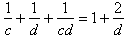 ,
,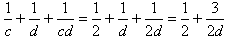 ,
,