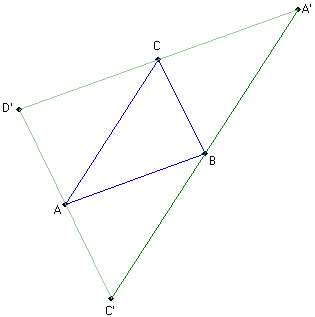
ABA'C,
ABCD',
AC'BC.
LIGA ZADANIOWA UMK W TORUNIU 2002/2003
PREZENT WAKACYJNY
DLA UCZNIÓW GIMNAZJUM
Zadanie 13
Na płaszczyźnie dane są trzy punkty nie leżące na jednej prostej. Ile istnieje równoległoboków, których trzy wierzchołki pokrywają się z danymi punktami.Rozwiązanie:
|
Mając dane trzy punkty A, B, C nie leżące na jednej prostej możemy skonstruować trzy równoległoboki zawierające punkty A, B, C jako wierzchołki: ABA'C, ABCD', AC'BC. |
|
Odpowiedz:
Istnieją trzy takie równoległoboki, których trzy wierzchołki pokrywają się z danymi punktami.Magda Nieżurawska