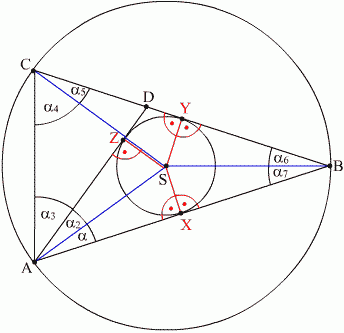
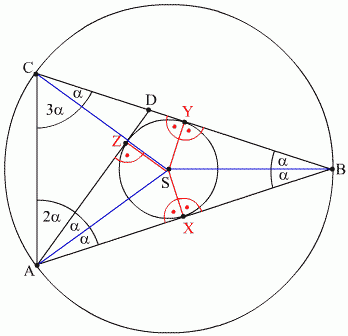
- Trójkąty AZS, AXS, BXS, BYS, CSY są przystające, więc
a = a2 = a6 = a7 = a5
- AD jest dwusieczną kąta BAC więc
a3 = a + a2 = a + a = 2a
- Trójkąt ASC jest równoramienny, więc
a4 = a2 + a3 = a + 2a = 3a
LIGA ZADANIOWA UMK W TORUNIU 2002/2003
PREZENT WAKACYJNY
DLA UCZNIÓW GIMNAZJUM
Zadanie 19
W trójkącie ABC poprowadzono dwusieczną AD. Wyznaczyć miary kątów trójkąta ABC jeśli środek okręgu wpisanego w trójkąt ABD jest jednocześnie środkiem okręgu opisanego na trójkącie ABC.Rozwiązanie
Przyjmijmy oznaczenia jak na rysunku.
|
 |
 |
|
Odpowiedź
Miary kątów trójkąta ABC wynoszą 36°, 72° i 72°.Paweł Rzymyszkiewicz