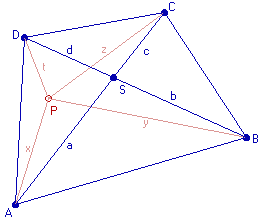
Niech S będzie punktem przecięcia się przekątnych czworokąta ABCD
oraz niech P będzie dowolnym punktem wewnątrz tego czworokąta różnym od S.
Z nierówności trójkąta:
x+z > a+c
t+y > b+d
Stąd: x+z+t+y > a+c+b+d
LIGA ZADANIOWA UMK W TORUNIU 2002/2003
PREZENT WAKACYJNY
DLA UCZNIÓW GIMNAZJUM
|
Przyjmijmy oznaczenia jak na rysunku. Niech S będzie punktem przecięcia się przekątnych czworokąta ABCD oraz niech P będzie dowolnym punktem wewnątrz tego czworokąta różnym od S. Z nierówności trójkąta: x+z > a+c Stąd: x+z+t+y > a+c+b+d |
 |
Artur Rasztubowicz