LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

Zadanie 6

Wyznacz pole czworokąta ABCD, mając współrzędne punktów A = (-1,-3), B = (-4,1), C = (8,6), D = (6,-1).

Rozwiązanie

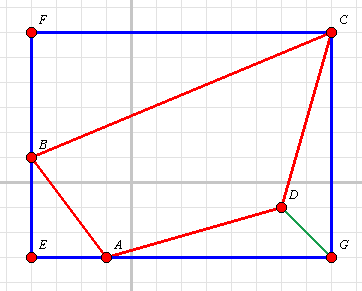Rysujemy najmniejszy czworokąt, w który "zmieści" się czworokąt ABCD.


Rysujemy odcinek DG.


Zauważmy, że powstały 4 trójkąty:
BCF, ABE, AGD, GDC.


Zatem pole ABCD będzie się równało:

PABCD = PEGCF - PBCF - PABE - PAGD - PGDC

PEGCF =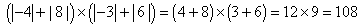

PBCF =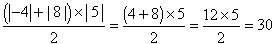

PABE =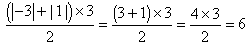

PAGD =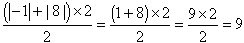

PGDC =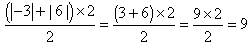

Czyli pole czworokąta ABCD równa się:

PABCD = 108 - 30 - 6 - 9 - 9 = 54

Odpowiedź

Pole czworokąta ABCD wynosi 54 jednostki kwadratowe.

Michał Kęder