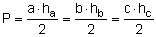LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS VI SZKÓŁ PODSTAWOWYCH
Zadanie 12
Zadanie 6
Czy istnieje trójkąt o wysokościach 6cm, 3cm i 2cm?
Rozwiązanie
Niech
ha = 6cm
hb = 3cm
hc = 2cm
Pole trójkąta wynosi:
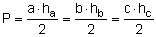
Aby trójkąt istniał jego dwa boki muszą być dłuższe od trzeciego: a + b > c, a + c > b, b + c > a.
Policzmy więc długości boków

Gdzie x to a, b lub c.
Sprawdźmy teraz każdy z przypadków.
I przypadek
b + c > a

Podstawmy zamiast ha - 6, hb - 3, hc - 2

Widzimy, że b + c jest większe od a. Sprawdźmy kolejny przypadek.
II przypadek
a + c > b

Podstawmy zamiast ha - 6, hb - 3, hc - 2

Widzimy, że a + c jest większe od b. Sprawdźmy kolejny przypadek.
III przypadek
a + b > c

Podstawmy zamiast ha - 6, hb - 3, hc - 2

Widzimy, że a + b nie jest większe (tylko równe) od c. Czyli taki trójkąt nie istnieje.
Odpowiedź
Taki trójkąt nie istnieje.
Michał Kęder