LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
Zadanie 6
W trójkącie prostokątnym przyprostokątne mają długości 15 cm i 20 cm. Oblicz długości odcinków na jakie przeciwprostokątną dzieli wysokość opuszczona z wierzchołka kąta prostego.Rozwiązanie
Z twierdzenia Pitagorasa obliczamy długość przeciwprostokątnej: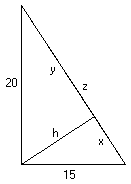 Następnie obliczamy pole trójkąta:
Następnie obliczamy pole trójkąta:Odpowiedź
Długości odcinków na jakie przeciwprostokątną dzieli wysokość opuszczona z wierzchołka kąta prostego wynoszą 9 cm i 16 cm.Michał Kęder