LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
Zadanie 6
Ile jest liczb naturalnych nieparzystych jedenastocyfrowych,
z których każda jest podzielna przez 9 i w zapisie dziesiętnym jej występują jedynie cyfry 0 i 5?
Rozwiązanie
W liczbach naturalnych nieparzystych, składających się tylko z zer i piątek, ostatnią cyfrą będzie na pewno 5.
Ponieważ pierwszą cyfrą liczby nie może być 0, to będzie nią też 5.
Nasze liczby będą więc wyglądały następująco:
5 x x x x x x x x x 5
gdzie x to albo 0 albo 5.
Jeżeli liczba jest podzielna przez 9, to suma jej cyfr jest podzielna przez 9.
Jedynym przypadkiem kiedy liczba jedeneastocyfrowa jest podzielna przez 9 jest więc liczba zawierająca dziewięć 5 i dwa 0.
Pozostaje odpowiedzieć na pytanie na ile sposobów można dwa zera rozmieścić w ciągu dziewięciu cyfr (nie jedenastu, ponieważ na początku i na końcu musi być 5).
Można to rozwiązać korzystając z dwumianu Newtona.
Wybieramy 2 elementy z 9, więc wzór będzie wyglądał następująco:
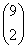
Po rozwiązaniu
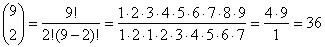
widzimy, że jest 36 takich możliwości, więc tyle samo jest poszukiwanych liczb.
Odpowiedź
Takich liczb jest 36.
Michał Kęder