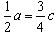 wynika, że
wynika, że 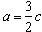 , więc c dzieli się przez 2.
, więc c dzieli się przez 2.LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS VI SZKÓŁ PODSTAWOWYCH
Wodę z baku wlano do każdego pojemnika po równo.

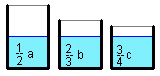
Wszystkie liczby a, b, c są całkowite.
Z równania 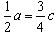 wynika, że
wynika, że 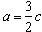 , więc c dzieli się przez 2.
, więc c dzieli się przez 2.
Z równania 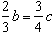 wynika, że
wynika, że  , więc c dzieli się przez 8.
, więc c dzieli się przez 8.
Najmniejszą liczbą całkowitą podzielną przez 2 i 8 jest liczba 8, więc c = 8.
Wtedy 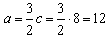 ,
, 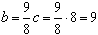
oraz 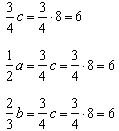
Zatem najmniejsza możliwa pojemność baku wynosi 3 × 6 = 18
Marcin Kopczyński