LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
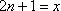
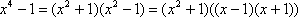
.gif)
Jeśli n jest nieparzyste to:
n2 - nieparzyste
a ponieważ n(n+1)=n2+n to mamy do czynienia z sumą liczb nieparzystych, a
l. nieparzysta + l. nieparzysta = l. parzysta
jeśli z kolei n jest parzyste to:
n2 - parzyste
a wiec mamy do czynienia z sumą liczb parzystych,a
l. parzysta + l. parzysta = l. parzysta
a liczby parzyste dziela się przez 2
Tak więc jeśli liczba naturalna n jest nieparzysta, to różnica jej czwartej potęgi i liczby 1 jest podzielna przez 16.
cnd.
Marcin Kopczyński