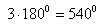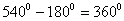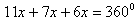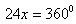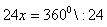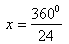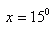LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS I GIMNAZJUM
Zewnętrzne kąty trójkąta są proporcjonalne do liczb 6:7:11.
Znajdź kąt między wysokościami wychodzącymi z
wierzchołków mniejszych kątów wewnętrznych tego trójkąta.
Oznaczamy odpowiednie kąty
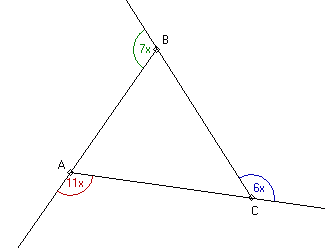
Obliczamy sumę kątów zewnętrznych trójkąta ABC:
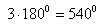
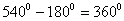
Aby dowiedzieć się jakie miary mają miary kąty zewnętrzne tego trójkąta obliczamy x:
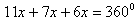
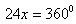
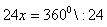
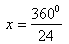
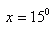
Obliczamy miary kątów:
11x = 11 × 15° = 165°
7x = 7 × 15° = 105°
6x = 6 × 15° = 90°
Obliczamy miary kątów wewnętrznych trójkąta ABC:
|ĐBAC| = 180° - 165°= 15°
|ĐABC| = 180° - 105°= 75°
|ĐACB| = 180° - 90°= 90°
Ponieważ jest to trójkąt prostokątny więc miara kąta między wysokościami
wychodzącymi z wierzchołków mniejszych kątów będzie wynosiła 90°
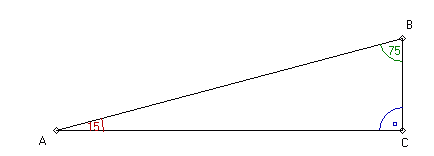
Miara kąta znajdującego się pomiędzy wysokościami
wychodzącymi z mniejszych kątów wewnętrznych tego trójkąta wynosi 90°.
Agata Kozińska