LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
Zadanie 8
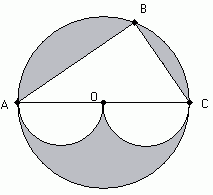
Średnica AB dzieli koło o środku O na dwie części. Trójkąt jest prostokątny i jego przyprostokątne mają długości 16cm i 12cm. Na odcinkach AO i OB. jako na średnicach skonstruowano półkola leżące na zewnątrz trójkąta ABC (patrz rysunek). Oblicz pole i obwód zacieniowanego obszaru.
Rozwiązanie:
Wprowadzamy oznaczenia:
Pz - pole zacieniowanej figury
Po - pole dużego koła
Po1 - pole małego koła
P> - pole trójkąta
Pz = Po - (P> + Po1)
Obw.z = Obw.o + Obw.o1 + |AC| + |BC|
Z Twierdzenia Pitagorasa obliczamy
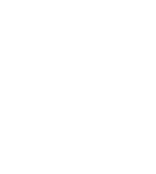
Obliczamy pole trójkąta:
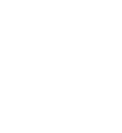
Obliczamy długość promieni małych okręgów:
średnica małego okręgu jest równa promieniowi dużego okręgu:
20cm : 2="10cm
natomiast promień małego okręgu to połowa jego średnicy, więc:
10cm : 2="5cm
Obliczamy pole małego koła:
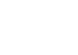
Obliczamy pole dużego koła:
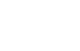
Obliczamy pole zacieniowanej figury:
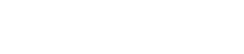
Obliczamy obwód zacieniowanej figury:
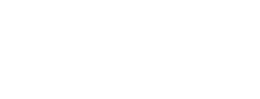
Odpowiedź: Pole zacieniowanej figury wynosi  , a jej obwód
, a jej obwód 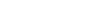
Agata Kozińska

 , a jej obwód
, a jej obwód