LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS VI SZKÓŁ PODSTAWOWYCH
Zadanie 9
Liczba naturalna n równa jest sumie pewnych trzech różnych dzielników liczby n - 1. Wyznacz wszystkie liczby n o tej własności.
Rozwiązanie
Niech d1, d2, d3 oznaczają parami różne dzielniki liczby n - 1 ustawione największego do największego, tzn. d1 > d2 > d3
i niech n = d1 + d2 + d3
Niech 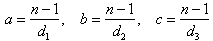 .
.
Liczby a, b, c są naturalne, a < b < c
i 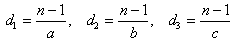 .
.
Wtedy
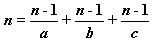
Możemy wynieść n - 1 przed nawias:
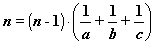
Możemy obie strony równania podzielić przez n - 1:
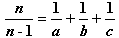
a więc 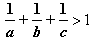
Popatrzmy jakie kolejne 3 wartości od największej do najmniejszej może przyjmować 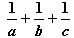 :
:
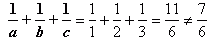 za dużo. za dużo.
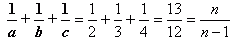 pasuje. pasuje.
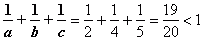 to za mało. to za mało.
|
Dalsze wartości 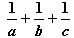 będą jeszcze mniejsze więc nie będą spełniać warunków zadania.
będą jeszcze mniejsze więc nie będą spełniać warunków zadania.
Ostatecznie wynika stąd, że jedyną liczbą spełniającą warunki zadania jest n = 13.
Paweł Kruszka
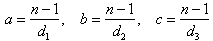 .
.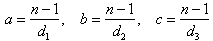 .
.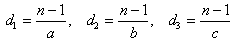 .
.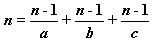
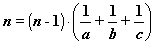
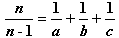
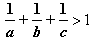
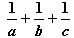 :
:
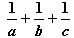 będą jeszcze mniejsze więc nie będą spełniać warunków zadania.
będą jeszcze mniejsze więc nie będą spełniać warunków zadania.