LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

ZADANIE 13

Na okręgu obierz trzy punkty A, B, C tak, aby powstał trójkąt prostokątny, a miara kąta ostrego CAB wynosiła 30°. Oblicz miary kątów środkowych opartych na łukach wyznaczonych przez przyprostokątne AC oraz BC trójkąta prostokątnego .

ROZWIĄZANIE:

Wstępny szkic

Trójkąt prostokątny z kątem 30° jest połową trójkąta równobocznego. Zatem bok naprzeciwko kąta 30° jest dwa razy krótszy od przeciwprostokątnej.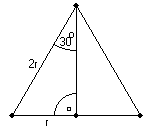

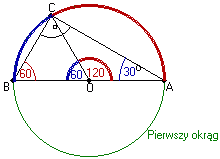
Konstrukcja trójkąta w okręgu

  1. Rysujemy więc (pierwszy) okrąg.
  2. Na okręgu zaznaczamy w dowolnym miejscu punkt A.
  3. Z punktu A rysujemy średnicę i jej drugi koniec oznaczamy przez B.
  4. Z punktu B rysujemy drugi okrąg o tym samym promieniu co okrąg pierwszy.
  5. Zaznaczamy punkt przecięcia się narysowanych okręgów i oznaczamy go przez C.

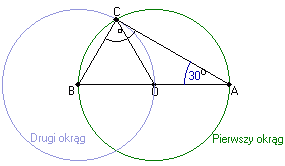
Miary kątów

  1. Miara kąta wpisanego opartego na łuku AC wynosi:
    |ĐABC| = 180° - 90° - 30° = 60°.
  2. Kąt środkowy oparty na łuku AB jest dwa razy większy niż kąt wpisany oparty na tym samym łuku:
    |ĐAOC| = 2×|ĐABC| = 2×60° = 120°.
  3. Kąt środkowy oparty na łuku BC jest dwa razy większy niż kąt wpisany oparty na tym samym łuku:
    |ĐBOC| = 2×|ĐBAC| = 2×30° = 60°.

ODPOWIEDŹ:

Miary kątów środkowych opartych na łukach wyznaczonych przez przyprostokątne AC oraz BC trójkąta prostokątnego ABC wynoszą odpowiednio 120° i 60°.

Marcin Pezda