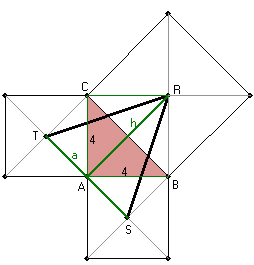
Przyjmując oznaczenia jak na rysunku, mamy policzyć pole P trójkąta SRT o podstawie a = |ST| i wysokości h = |AR| = |BC|.
Z tw. Pitagorasa (patrz: trójkąt ABC):h2 = 42 + 42
h2 = 16 × 2
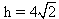
Łatwo zauważyć, że 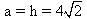 .
.
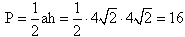
LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 14
Na zewnątrz trójkąta prostokątnego równoramiennego o przyprostokątnej długości 4 cm zbudowano kwadraty. Jednym z boków każdego kwadratu jest bok tego trójkąta. Punkty przecięcia przekątnych kwadratów wyznaczają trójkąt. Oblicz pole otrzymanego trójkąta.Rozwiązanie
Przyjmując oznaczenia jak na rysunku, mamy policzyć pole P trójkąta SRT o podstawie a = |ST| i wysokości h = |AR| = |BC|. Z tw. Pitagorasa (patrz: trójkąt ABC):h2 = 42 + 42 h2 = 16 × 2 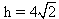
Łatwo zauważyć, że
|
 |
Odpowiedź
Pole trójkąta wynosi 16 cm2.Michał Pośpiech
Marzec 2003