LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS VI SZKÓŁ PODSTAWOWYCH
Zadanie 19
W trójkącie prostokątnym ABC z kątem prostym przy wierzchołku C poprowadzono wysokość CH. Wyznacz miary kątów tego trójkąta, jeśli wiadomo, że |HB| - |AH| = |AC|.
ROZWIĄZANIE
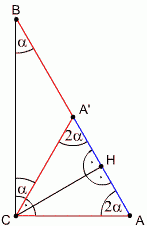 |BH|-|AH|=|AC|
|BH|-|AH|=|AC|ODPOWIEDŹ
Miary kątów w tym trójkącie mają miary 30°, 60° i 90°.