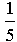LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

Zadanie 20

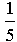Oblicz miary kątów trójkąta równoramiennego, którego wierzchołki leżą na okręgu wiedząc, że jeden z boków jest oparty na długości okręgu.

Przyjmijmy oznaczenia jak na rysunku. Kąt środkowy oparty na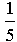 okręgu ma miarę 360°:5 = 72°. Trójkąt AOB jest równoramienny oraz: 2x + 72° = 180° 2x = 108° x = 54° Trójkąty AOC i BOC są równoramienne oraz: 4y + 2x = 180° 4y + 108°= 180° 4y = 72° y = 18°

Kąty w trójkącie ABC mają zatem następujące miary:

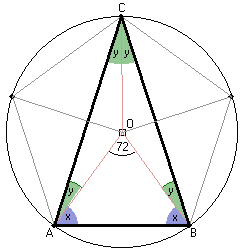|ĐBAC| = |ĐABC| = x + y = 54° + 18° = 72°.

|ĐACB| = = 2y = 2×18° = 36°

.

Miary trójkąta są równe: 72°, 72° i 36°.

Paweł Sobociński