 P="?" Obw="?"
P="?" Obw="?" LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA KONKURSOWE Z ETAPU III
DLA KLAS II GIMNAZJUM
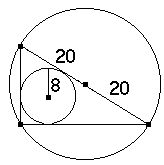
Wyznaczyć pole i obwód trójkąta prostokątnego, w którym długość promienia okręgu wpisanego wynosi 8 cm, a długość promienia okręgu opisanego na tym trójkącie jest równa 20 cm.
 P="?" Obw="?"
P="?" Obw="?"
Rozwiązanie:
Korzystam z prawa, mówiącym o tym, że suma długości średnic okręgu wpisanego i opisanego na dowolnym trójkącie prostokątnym jest równa sumie długości przyprostokątnych tego trójkąta.
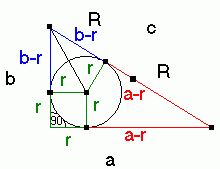
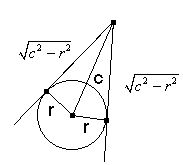
2R = b-r + a-r
2R + 2r = b+a
a+b = 2 (R+r)
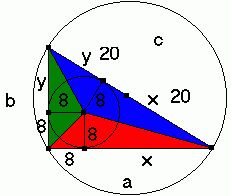
Obw = 2y + 2x + 2*8 = 2 (x+y) + 16 = 2*40 + 16 = 96
W trójkącie prostokątnym da się zauważyć wyraźne 3 trójkąty. Suma ich pól równa się polu trójkąta prostokątnego.
P = 1/2*a*8 + 1/2*b*8 + 1/2*c*8 = 1/2*8* (a+b+c) = 1/2*8*obwód = 1/2*8*96 = 384
Odp.: Pole = 384, obwód = 96
Paweł Sobociński