LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS VI SZKÓŁ PODSTAWOWYCH
Zadanie 22
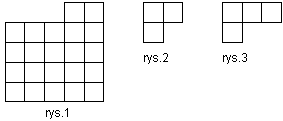
| Nauczyciel rozciął figurę przedstawioną na rys. 1 na figury o kształtach przedstawionych na rys. 2 i rys. 3. Ile figur o kształcie przedstawionym na rys. 2 mógł otrzymać przy tym podziale? |  |
Rozwiązanie
Figura na rys. 1 składa się z 22 kwadracików.Warianty:
18 : 3 = 6, to znaczy, że figur składajacych się z 3 kwadracików musi być sześć.
Nauczyciel może rozciąć tę figurę w następujący sposób: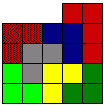
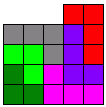
Odpowiedź
Po rozcięciu figury z rysunku nr. 1 można otrzymać 2 lub 6 figur przedstawionych na rys. 2.Paulina Szewczyk