Zadanie 4
Na rysunku obok punkty A, B, C, D, E dzielą okrąg na równe części. Oblicz miary kątów CAD, CDE oraz CFB.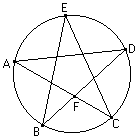
LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA KONKURSOWE Z ETAPU II
DLA KLAS I GIMNAZJUM
Zadanie 4 Na rysunku obok punkty A, B, C, D, E dzielą okrąg na równe części. Oblicz miary kątów CAD, CDE oraz CFB. |  |
Rozwiązanie
Z treści zadania wynika, że wielokąt ABCDE jest pięciokątem foremnym.| W pięciokącie suma miar kątów wewnętrznych wynosi 3×180° = 540°. W pięciokącie foremnym wszystkie kąty są równe więc miara każdego z nich jest równa 540°:5 = 108°. Zatem Trójkąt CDE jest równoramienny więc każdy zielony kąt ma miarę Wynika stąd, że oraz | 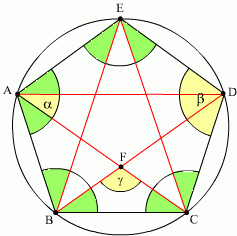 |
Odpowiedź
Katy CAD, CDE oraz CFB mają kolejno miary: 36°, 108° oraz 108°.Piotr Tylenda