LIGA ZADANIOWA UMK W TORUNIU 2002/2003
ZADANIA KONKURSOWE Z ETAPU III
DLA KLAS I GIMNAZJUM

Zadanie 6

Oblicz pole wielokąta przedstawionego na rysunku wiedząc, że 0< x <1.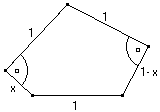

Rozwiązanie     (Patrz także --> Drugie rozwiązanie bez rachunków)

Dzielę pięciokąt na trzy trójkąty

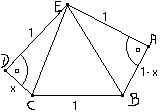
Opuszczam wysokość na bok CB.

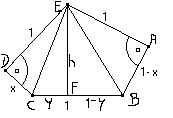
Otrzymaliśmy następujące układy równań:

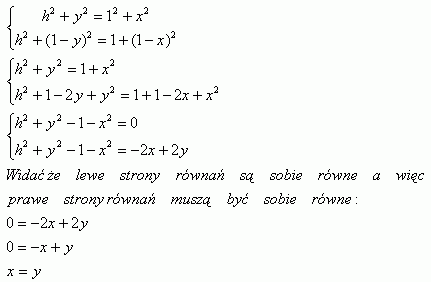
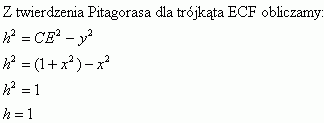
Więc z cechy BBB zauważamy, iż trójkąty EFC i DEC są przystające oraz trókąty EFB i EBA są przystające.

Obliczam pole trójkata CED. Skoro jest to trójkąt prostokątny to jego wysokością jest odcinek CD. Więc pole trójkąta CED wynosi:

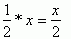
Następnie obliczam pole trójkąta ABE:

Pole tego pięciokąta wynosi:

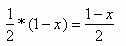
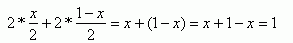
Odpowiedź

Pole tego wielokąta wynosi 1

Iwona Lis