LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS II GIMNAZJUM
Zadanie 11
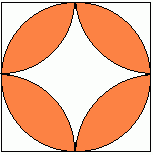
W kwadracie o boku długości 10 cm (patrz rysunek obok) można zauważyć okrąg wpisany w ten kwadrat oraz ćwiartki czterech okręgów o promieniu 5 cm i środkach w wierzchołkach tego kwadratu. Oblicz pole i obwód zamalowanej figury

Rozwiązanie
Dany kwadrat o boku 10 cm dzielimy na 4 kwadraty o boku 5 cm. każdy z nich zawiera taką samą część figury w kształcie liścia.
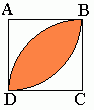
Prowadzimy odcinek z punktu B do punktu D:
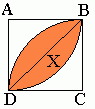
Trójkąt ADB jest prostokątny więc możemy przyjąć za jego podstawę bok AB, a za wysokość AD. Teraz obliczamy pole tego trójkąta:
P="1/2*5*5=1/2*25=25/2
Teraz obliczamy pole ćwiartki koła o środku A i promieniu 5 cm.
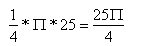
Następnie od pola ćwiartki koła odejmujemy pole trójkąta:
Otrzymujemy:
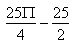
Ten wynik jest równy polu x
W tym kwadracie mamy 2 części x więc mnożymy ten wynik przez 2. Otrzymujemy:
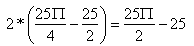
W zadaniu mamy 4 kwadraty więc wynik należy pomnożyć przez 4
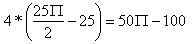
Obliczam obwód figury z zadania.
2*(2*P*5) = 20P
Odpowiedź
Pole zakreskowanej figury wynosi 50p-100, a obwód 10p.
Iwona Lis