LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
Zadanie:
Wyznaczyć pole i obwód ośmiokąta, w którym wszystkie kąty wewnętrzne są równe, zaś boki mają długości 1,
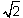 , 1,
, 1, 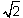 , 1,
, 1,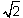 , 1,
, 1,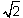 . w podanej kolejności.
. w podanej kolejności.
Rozwiązanie:
Dany jest kwadrat o boku 1/1. Jak powszechnie wiadomo, przekątna tego kwadratu
jest równa pierwiastek z dwóch. Wynika to z Tw. Pitagorasa:
a2 + b2 = c2
12 + 12 = c2
2 = c2
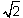 = c
= c
Korzystając z powyższych wlasności narysujmy dany ośmiokąt:
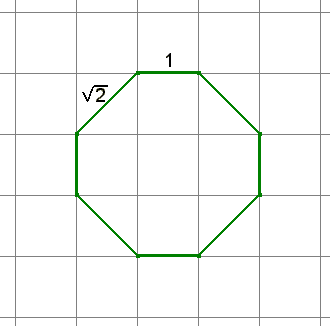
Z pomocą rysunku policzmy pole ośmiokąta:
P = 1 + 1 + 1 + 1 + 1 + 1/4 + 1/4 + 1/4 + 1/4
P = 6
Dzieje się tak ponieważ, na pole tej figury składają się:
- 4 trójkąty - każdy z nich to ćwiartka kwadratu o polu równym jeden;
- 5 kwadratów - każdy o polu równym jeden.
Natomiast obwód jest równy:
Obw = 4 + 4 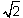
Odp:Pole tego ośmiokąta jest równe 6j2, a obwód (4 + 4 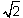 ) jednostek długości .
) jednostek długości .
Robert Chrzanowski
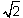 , 1,
, 1, 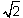 , 1,
, 1,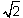 , 1,
, 1,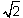 . w podanej kolejności.
. w podanej kolejności.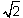 = c
= c
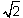
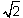 ) jednostek długości .
) jednostek długości .