LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS I GIMNAZJUM

Zadanie 6

Wyznaczyć wszystkie liczby pięciocyfrowe mające zpis dziesiętny abcde, które dzielą się przez 36 i dla których a < b < c < d < e.

Rozwiązanie

Muszą być spełnione następujące warunki: Skreślam cyfry niemożliwe:
1 Ł a < b < c < d < e Ł 9

Jeśli liczba abcde dzieli się przez 36, to również dzieli się przez 4, a więc jej dwie ostatnie cyfry muszą tworzyć liczbe podzielna przez 4.

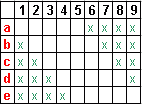
Liczba de musi dzielić się przez 4

de = 48 lub de = 68 lub de = 56

Jeśli liczba abcde dzieli się przez 36, to również dzieli się przez 9, w więc suma jej cyfr też musi dzielić się przez 9.

a + b + c + d + e
musi być podzielne przez 9 		Rozważam trzy możliwości dla de:
Jeśli de = 48,
to a = 1, b = 2, c = 3
1 + 2+ 3+ 4 + 8 = 18
abcde = 12348
Jeśli de = 68, to:
d + e = 14,
1 + 2 + 3 Ł a + b + c Ł 3 + 4 + 5
6 Ł a + b + c Ł  12
6 + 14 Ł a + b + c + d + e Ł  12 + 14
20 Ł a + b + c + d + e Ł  26
Między 20 a 26 nie ma liczby podzilenej przez 9, więc jest to
niemożliwe.
Jeśli de = 56, to:
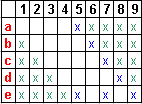
d + e = 11,
1 + 2 + 3 Ł a + b + c Ł 2 + 3 + 4
6 Ł a + b + c Ł 9
6 + 11 Ł a + b + c + d + e Ł  9 + 11
17 Ł a + b + c + d + e Ł  20
Między 17 a 20 tylko 18 dzieli się przez 9, więc:
a + b + c + d + e = 18
a + b + c = 7
a = 1, b = 2, c = 4
abcde = 12456

Odpoweidź

Możliwe liczby to: 12348 i 12456.

Radek Dąbrowski