LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS I GIMNAZJUM
Zadanie 7
Wśród wszystkich prostokątów o obwodzie 100 cm wyznacz ten, który ma największe pole. Odpowiedź uzasadnij.Rozwiązanie
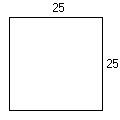
Chodzi o kwadrat:
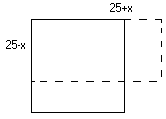
Jedynym kwadratem o obwodzie 100 jest kwadrat 25 × 25. Ma on pole równe 625. Kiedy do jednego z jego boków dodamy x, to - aby zachować obwód - od drugiego musimy odjąć x i wtedy pole nowo powstałego prostokąta będzie wynosiło 625 - x2 czyli mniej niż 625. |  |
| P = 25 · 25 = 625 | P = (25 + x) · (25 - x) = 625 - 25x + 25x - x2 = 625 - x2 |
Radek Dąbrowski