LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS I GIMNAZJUM

a) Ile soli należy wsypać do 12 kg wody, aby otrzymać czteroprocentową solankę?

b) Ile wody należy dodać do 6 kg pięcioprocentowej solanki, aby otrzymać solankę dwuprocentową?

c) Ile soli należy dosypać do 10 kg pięcioprocentowej solanki, aby otrzymać roztwór dwudziestoprocentowy?

a)

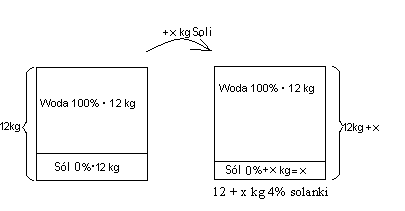
Kanister po lewej ilustruje sytuację początkową. Nie ma w nim soli, napisałem więc, że woda stanowi 100% jego zawartości. Po dosypaniu x kilogramów soli sytuację ilustruje kanister po prawej. Należy zwrócić uwagę, że ilość wody nie zmienia się, pojawia się natomiast sól, która stanowić teraz musi 4 procent zawartości kanistra.Należy teraz ułożyć równanie, które pomoże nam obliczyć x:

x = 4% (12 + x)

Oznacza to, że nowa ilość soli w kanistrze (x) równa się czterem procentom solanki o wadze 12 + x.

x = 4% (12 + x)      / ^.100 (by pozbyć się procentów)

100x = 4 (12 + x)

100x = 48 + 4x      / - 4x

96x = 48      / : 96

x = 0,5

Odp.Należy dosypać 0,5 kiliograma soli.

b)

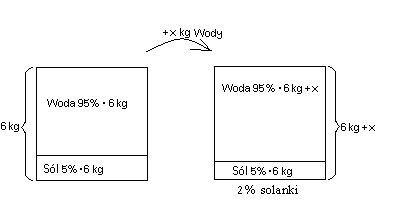
Kanister po lewej ilustruje sytuację początkową pokazując poporcję między wodą i solą. Po dolaniu x kilogramów wody, jej ilość (w kanistrze i samej sobie) wzrasta, nie zmienia się natomiast ilość soli.Tworzymy równanie:

95% ^. 6 + x = 98% (6 + x)

Oznacza to, że "nowa ilość wody" jest równa "roztworowi wody w soli" (Skoro ilość soli wynosi teraz 2%, to ilość wody to 98%).

95 ^. 6 + 100x = 98 (6 + x)

570 + 100x =588 + 98x      / - 570

100x = 18 + 98x      / - 98x

2x = 18      / : 2

x =9

Odp. Należy dolać dziewięć kilogramów wody.

c)

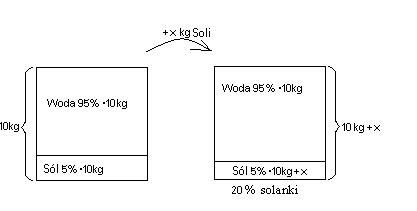
Kanister po lewej ilustruje sytuację początkową pokazując poporcję między wodą i solą. Po dosypaniu x kilogramów soli, jej ilość (w kanistrze i samej sobie) wzrasta, nie zmienia się natomiast ilość wody.Tworzymy równanie:

5% ^.10 + x = 20% (10 + x)

Oznacza to, że "nowa ilość soli" jest równa "roztworowi soli w wodzie" (Skoro ilość wody wynosi teraz 95%, to ilość soli to 5%).

5% ^.10 + x = 20% (10 + x)      / ^.100 (By pozbyć się procentów)

5^.10 + 100x = 20 (10 + x)

50 + 100x = 200 + 20x      / - 20x

50 + 80x = 200      / - 50

80x = 150      / : 80

x = 150 : 80

x = 1,875

Odp. Trzeba dosypać 1 kilogram i 875 gramów soli.

autor: Mateusz Gołaszewski