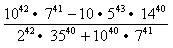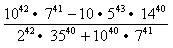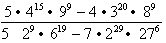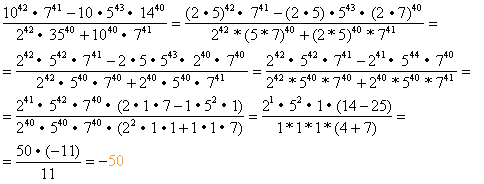LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS II GIMNAZJUM

Zadanie 7

Oblicz:

a: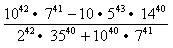

b: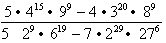

Rozwiązanie:

A

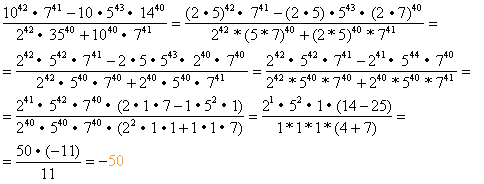
A oto, co kolejno tu robiłem:

• Korzystałem z możliwości zamienienia liczb złożonych na iloczyny liczb pierwszych (np.10⁴⁴ = (2*5)⁴²;
• Używałem prawa "Potęga iloczynów równa się iloczynowi potęg", np.(2*5)⁴² = 2⁴² * 5⁴²;
• Wynosiłem sobie przed nawias takie liczby, które były w liczniku lub mianowniku mniejsze ze swojej pary (to znaczy, że np. spośród liczb 2⁴¹ i 2⁴² to 2⁴¹ szło przed nawias);
• Skracałem odpowiednie potęgi z licznika i mianownika (a w nawiasach wykonałem proste już rachunki);
• Reszta poszła bardzo prosto...

B

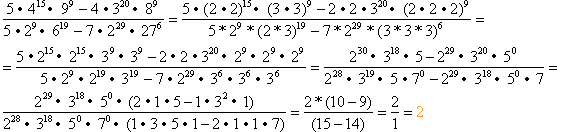
I znowu kolejność operacji:

• Korzystałem z możliwości zamienienia liczb złożonych na iloczyny liczb pierwszych (patrz przykład A);
• Dodawałem do siebie wykładniki potęg o tych samych podstawach. Ponadto, w odpowiednich miejscach dopisywałem zerowe potęgi pewnych liczb, tak, by później przy wynoszeniu przed nawias mieć odpowiednio "ładne" liczby (ostatecznie, i tak liczba naturalna podniesiona do potęgi zerowej da jeden (no chyba, że ta liczba to zero, ale tutaj oczywiście nie mamy takich możliwości i ponadto zera nie można podnosić do potegi zerowej));
• Wynosiłem sobie przed nawias takie liczby, które były w liczniku lub mianowniku mniejsze ze swojej pary (znowu patrz przykład A);
• Skracałem odpowiednie potęgi z licznika i mianownika (a to co w nawiasach policzyłem w pamięci);
• I dalej wszystko było jasne...

  Autor: Mateusz Gołaszewski