LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM

Zadanie 7

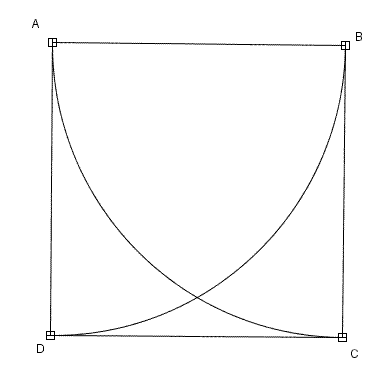
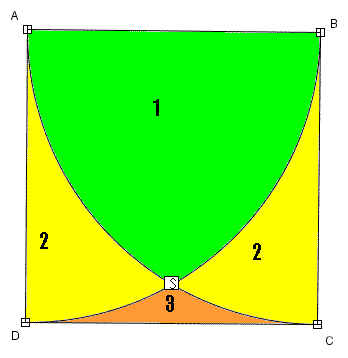
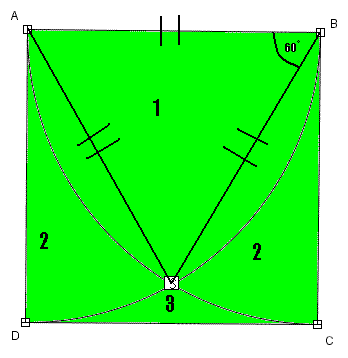
W kwadracie ABCD poprowadzono dwa okręgi o środkach w wierzchołkach A i B i o promieniu równym bokowi kwadratu. Okręgi te podzieliły kwadrat na cztery obszary. Oblicz pola i obwody tych obszarów, jeśli długość boku kwadratu jest równa 5 centymetrów.

Rozwiązanie:

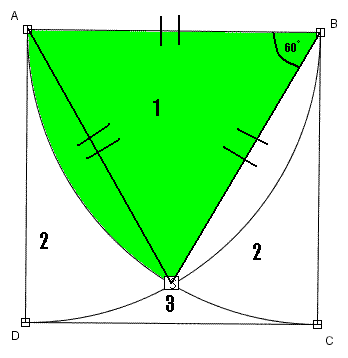
Należałoby zacząć od rysunku:

Trzeba też pamiętać o kilku wzorach:

a) Na pole koła: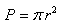

b) Na obwód koła: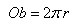

c) Na pole wycinka koła: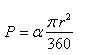

d) Na długość łuku: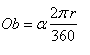

e) Na pole trójkąta równobocznego: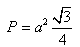

Gdzie r to promień koła, zaś a to kąt wpisany w koło, na którym oparty jest łuk.

Zaczniemy od policzenia pola oznaczonego jedynką:

Najpierw rysujemy dwa odcinki: AS i BS, w ten sposób uzyskując trójkąt równoboczny ABS:

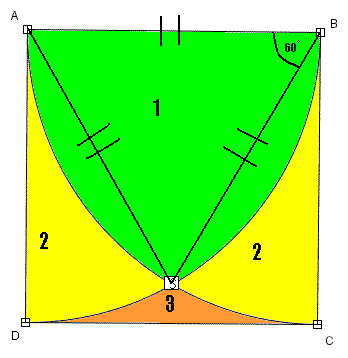
Skąd to wiemy? Zauważamy, że boki AS i BS "odchylają" się jakby od boków AD i BC po łukach DS i CS. A jak wiadomo, |AB|=|AD|=|BC|.

Teraz liczymy pole trójkąta równobocznego ABS. Ze wzoru piątego wiemy, że będzie to .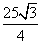

Następnie obliczamy pole wycinka koła ABS:

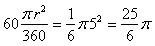
Teraz musimy poznać pole "listka", czyli tego "dwuboku" AS. Jak wiemy, będzie to pole wycinka koła ABS minus pole trójkąta ABS, czyli .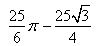

Teraz już łatwo zauważyć, że pole pierwszej figury równa się polu trójkąta ABS plus dwóm polom "listków", czyli .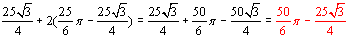

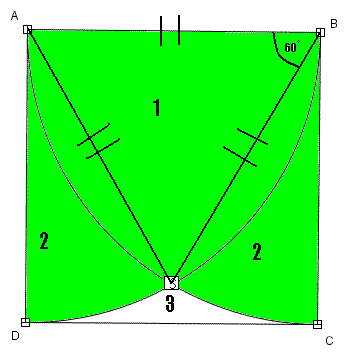
Teraz czas na pole numer 2:

Można je przedstawić jako pole ćwiartki koła:

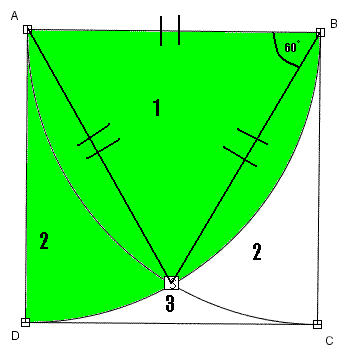
minus pole 1:

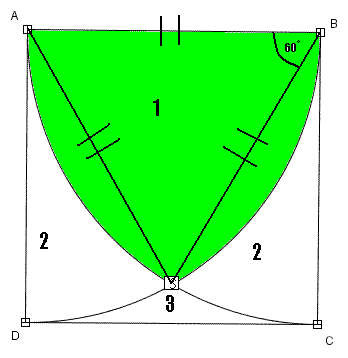
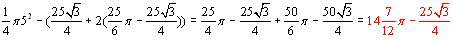
Zostaje jeszcze pole numer trzy. Tutaj będzie najłatwiej, gdyż równa się ono polu całego kwadratu:

minus pole numer 1 i dwa pola numer 2:

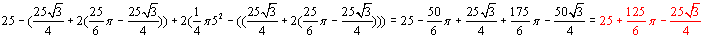
Odpowiedź: Pierwsze pole równe jest 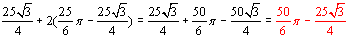, drugie pole równe jest równe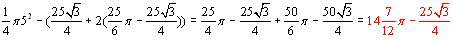, zaś trzecie jest równe .

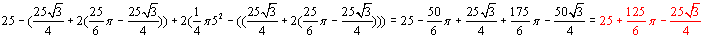Autor: Mateusz Gołaszewski