LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS I GIMNAZJUM
Zadanie 9
Uzasadnij, że ułamek 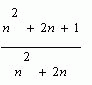 jest nieskracalny.
jest nieskracalny.
Rozwiązanie
Ułamek można skrócić tylko przez wspólny dzielnik licznika i mianownika.
Ułamek jest skracalny, jeśli licznik i mianownik
mają jakiś wspólny dzielnik naturalny większy niż 1.
- Jeśli licznik n2 + 2n + 1 i mianownik n2 + 2n dzielą się przez wspólną liczbę naturalną d,
to ich różnica też dzieli się przez d.
- (n2 + 2n + 1) - (n2 + 2n) = 1, więc 1 dzieli się przez d.
- Ponieważ jedyną liczbą naturalną, przez którą dzieli się liczba 1 jest 1, więc d = 1.
Wynika stąd, że podany ułamek jest nieskracalny.
Mateusz Grącki
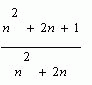 jest nieskracalny.
jest nieskracalny.