LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA WAKACYJNE
DLA UCZNIÓW GIMNAZJUM

Zadanie 9

Pierwszą cyfrą pewnej liczby jest 7. Cyfrę tę przeniesiono na koniec i wówczas otrzymano liczbę dwukrotnie mniejszą. Co to za liczba?

Rozwiązanie

Liczba z cufrą 7 na końcu jest dwa razy mniejsza od tej z cyfrą 7 na początku.
Więc gdy pomnożymy tę z 7 na końcu to otrzymamy tę z 7 na początku. Pisemnie będzie to wyglądało tak:

Od razu widać, że ostatnia cyfra wyniku musi być 4 bo 7×2 = 14 i trzeba wpisać 4 (i mieć 1 w pamięci).

Teraz 2×4 = 8 i 1 w pamięci, to daje 9. Wpisujemy 9:

I tak dalej. Po wielu obliczeniach dotrzmy do cyfry 7 nie mając juz nić w pamięci. Pierwszy raz będzie to liczba 18 cyfrowa gdzie siódemka jest bez żadnej 1 w pamięci:


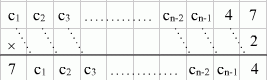
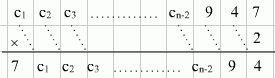
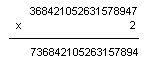
Tu zamieszczone są wszystkie obliczenia:

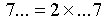Komentarz
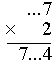2×7 = 14
Wpisujemy 4,
w pamięci mamy 1.
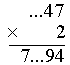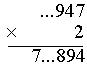Rozmiar: 263 ></TD> <TD>2×4 + 1 = 9<BR>Wpisujemy 9.<BR></TD></TR> <TR> <TD ALIGN= 2×9 = 18
Wpisujemy 8,
w pamięci mamy 1.
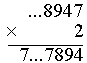2×8 + 1 = 17
Wpisujemy 7,
w pamięci mamy 1.
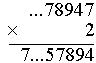2×7 + 1 = 15
Wpisujemy 5,
w pamięci mamy 1.
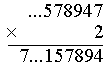2×5 + 1 = 11
Wpisujemy 1,
w pamięci mamy 1.
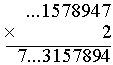2×1 + 1= 3
Wpisujemy 3.
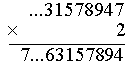2×3 = 6
Wpisujemy 6.
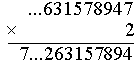2×6 = 12
Wpisujemy 2,
w pamięci mamy 1.
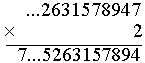2×2 + 1 = 5
Wpisujemy 5.
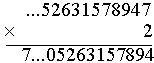2×5 = 10
Wpisujemy 0,
w pamięci mamy 1.
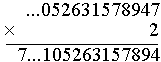2×0 + 1 = 1
Wpisujemy 1.
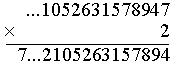2×1 = 2
Wpisujemy 2.
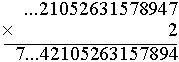2×2 = 4
Wpisujemy 4.
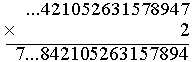2×4 = 8
Wpisujemy 8.
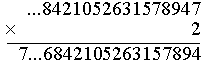2×8 = 16
Wpisujemy 6,
w pamięci mamy 1.
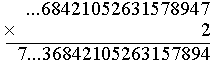2×6 + 1 = 13
Wpisujemy 3,
w pamięci mamy 1.
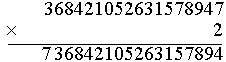2×3 +1 = 7
Dotarliśmy cyfry 7.
To jest właściwa liczba.

Odpowiedź

Jest to liczba 736842105263157894.

Mateusz Grącki

PS. Gdybym dalej kontynuował obliczenia to otrzymałbym podobnie liczbę, w której 2 razy powtórzyłby się ten sam ciąg cyfr. Byłaby to liczba 36 cyfrowa

736842105263157894736842105263157894

Mogę to zrobić jeszcze raz i jeszcze, powtarzając ten sam ciąg cyfr tyle razy ile mi się będzie chciało i też wynik będzie poprawny.