- Jeśli n = 2, to
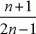 = 1 - to jest liczba całkowita
= 1 - to jest liczba całkowita
- Jeśli n = 1, to
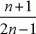 = 2 - to też jest liczba całkowita.
= 2 - to też jest liczba całkowita.
- Jeśli n = 0, to
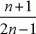 = -2 - i to też jest liczba całkowita.
= -2 - i to też jest liczba całkowita.
liGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA WAKACYJNE
DLA UCZNIÓW GIMNAZJUM
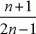 była liczba całkowitą.
była liczba całkowitą.
|
n + 1 ≥ 2n - 1 / -1 n ≥ 2n - 2 /-2n -n ≥ - 2 /·(-1) n ≤ 2 |
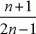 = 1 - to jest liczba całkowita
= 1 - to jest liczba całkowita
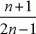 = 2 - to też jest liczba całkowita.
= 2 - to też jest liczba całkowita.
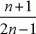 = -2 - i to też jest liczba całkowita.
= -2 - i to też jest liczba całkowita.Szukane liczby to 0, 1 i 2.
Rozwiązała Magdalena Jastrzembska