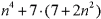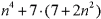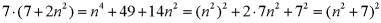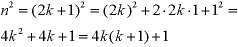LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS II GIMNAZJUM
ZADANIE 10
Uzasadnij, że jeśli n jest liczbą nieparzystą, to liczba
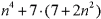
jest podzielna przez 64.
Rozwiązanie
- Doprowadźmy to równanie do postaci (a+b)2:
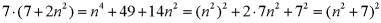
- Z założenia, że n jest liczbą nieparzystą wynika, że n = 2k + 1 gdzie k jest liczbą całkowitą. Wobec tego:
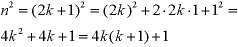
Któraś z liczb k lub k+1 jest parzysta, bo to są dwie kolejne liczby całkowite, a więc k(k+1) jest na pewno liczbą parzystą. Stąd:
4k(k+1) dzieli się przez 8,
4k(k+1)= 8l gdzie l jest liczbą całkowitą.
- Ostatecznie:
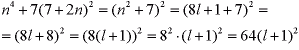
Rozwiązała Magdalena Jastrzembska.