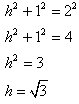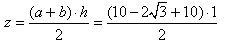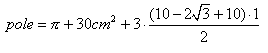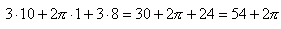LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS II GIMNAZJUM
Zadanie 10
Brzeg trójkąta równobocznego o boku długości 10 cm ,,otoczono" zbiorem wszystkich punktow, które są odległe od co najmniej jednego z boków nie więcej niż o 1 cm. Oblicz pole tego zbioru oraz długość jego brzegu.
Rozwiązanie:
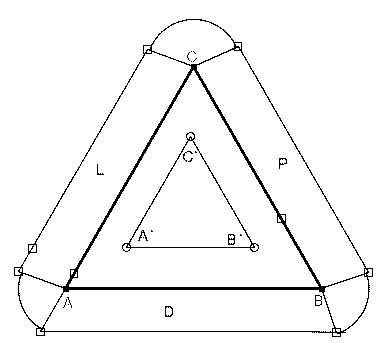
Otoczenie trójkąta ABC od jego zewnętrzenj strony zewnętrznej składa się z 6 segmentów- 3 prostokatów i 3 wycinków koła (które razem tworzą jedno koło).
Brzeg otoczenia tr. ABC od strony wewnętrznej jest trójkątem równobocznym.Pole otoczenia zewnętrznego jest więc równe:
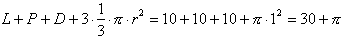
Wewnętrzna granica zbioru punktów spełniających warunki zadania składa się z 3 trapezów, tak jak widać na poniższym rysunku.
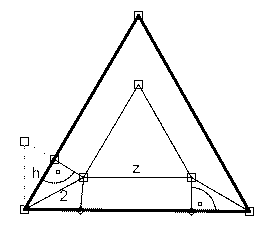 rys.1 Wewnętrzna granica
rys.1 Wewnętrzna granica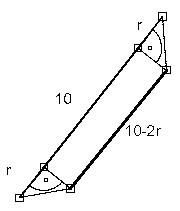 rys.2 Trapez
rys.2 Trapez
Z twierdzenia Pitagorasa (c2=a2+b2)Wynika że:
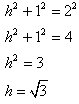
Korzystając z wzoru na pole trapezu liczymy, ile wynosi pole jednego z nich. Oznaczmy go literą z:
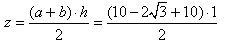
W takim razie pole całej zacieniowanej figury wynosi:
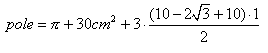
Teraz policzmy długość jego brzegu ( UWAGA: DO DŁUGOŚCI TEGO BRZEGU ZALICZAMY I ZEWNĘTRZNĄ GRANICĘ I WEWNĘTRZNĄ GRANICĘ!)
Długość brzegu, równa się:
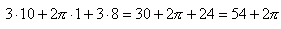
Rozwiązała Magdalena Jastrzembska
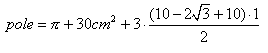

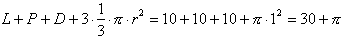
 rys.1 Wewnętrzna granica
rys.1 Wewnętrzna granica rys.2 Trapez
rys.2 Trapez