LIGA ZADANIOWA UMK W TORUNIU 2003/2004

LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA PRZYGOTOWAWCZE DO ETAPU II
DLA KLAS I GIMNAZJUM

Zadanie 15: Na okręgu o środku O zaznaczono punkty A, B i C tak, że kąt wpisany ABC ma miarę 40°, a kąt środkowy BOC ma miarę 160° (patrz rys.1). Oblicz miary kątów w trójkątach AOB, AOC, BOC (patrz rys.2).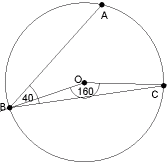

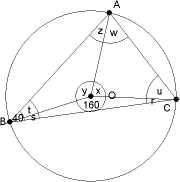rys.1 rys.1

Rozwiązanie

Kąty w trójkącie OCA:
Wiemy, że kąt wpisany jest 2 razy mniejszy od kąta środkowego opartego na ty samym łuku.
x=2*40°
x=80°

Odcinki OA, OB i OC są promieniami okręgu i mają równą długość, więc trójkąty BOA, BCO i CAO są równoramienne, a kąty przy ich podstawach są równe.
Skoro kąt pełny ma 360° to
w+u=180°-80°
w+u=100°
w i u są kątami przy podstawie
w=u
w=100°:2
w=50°
u=100°:2
u=50°

Kąty w trójkącie BOA:
y=360°-(x+160°)
y=360°-(80°+160°)
y=360°-240°
y=120°

t+z=180°-120°
t+z=60°
t i z są katmi przy podstawie.
t=z
t=60°:2
t=30°
z=60°:2
z=30°

Kąty w trójkącie BCO:
s+r=180°-160°
s+r=20°
s i r są kątami przy podstawie.
s=r
s=20°:2
s=10°
r=20°:2
r=10°

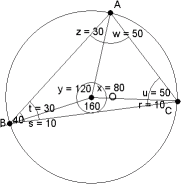
Odpowiedź: Kąt AOB ma 120°, kąt AOC ma 80°, kąt BOC ma 160°.

Anna Ługiewicz