LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA WAKACYJNE
DLA UCZNIÓW GIMNAZJUM
Zadanie 16: Wewnątrz czworokąta wypukłego znaleźć punkt, którego suma odległości od wierzchołków jest najmniejsza.
Rozwiazanie:
Pokażę, że jest to punkt przeciecia się przekątnych.
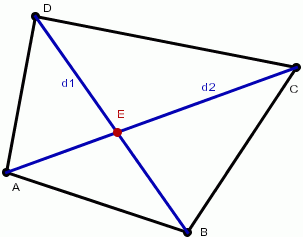
Dowód:
Zaznaczmy punkt P nie należący do żadnej przekątnej.
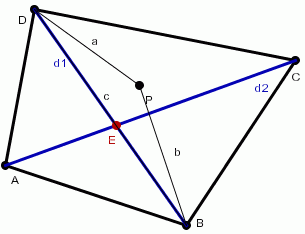
- Z nierówności trójkąta (patrz trójkąt BPD) wynika, że odcinki a + b > c , więc jeśli punkt P nie należy do przekątnej d1, jego suma odległości od wierzchołków D i B nie jest najmniejsza.
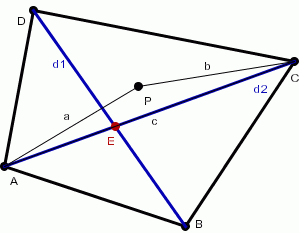
- Z nierówności trójkata (patrz trójkąt ACP) wynika, że odcinki a + b > c , więc jeśli punk P nie należy do przekątnej d2, jego suma odległości od wierzchołków A i C nie jest najmniejsza.
Aby punkt P należał do obu dwóch przekątnych musi być punktem ich przecięcia.
Odpowiedź: Punkt, którego suma odległości od wierzchołków jest najmniejsza jest punktem przeciecia się przekątnych.
Ania Ługiewicz



