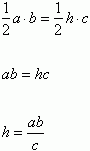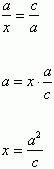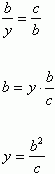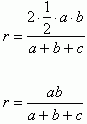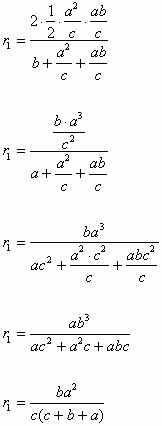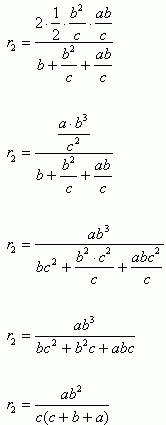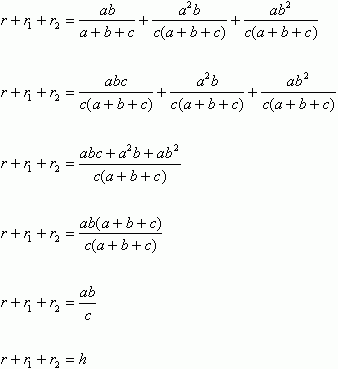LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM
Zadanie 16: W trójkącie prostokątnym ABC o kącie prostym przy wierzchłku C poprowadzono wysokość CD. Udowodnij, że r + r1 + r2 = h, gdzie r1 jest promieniem okręgu wpisanego w trójkąt ADC, r2 jest promieniem okręgu wpisanego w trójkąt DBC, a r promieniem okręgu wpisanego w trójkąt ABC, zaś h = |CD|.
Rozwiązanie:
Sposób I:
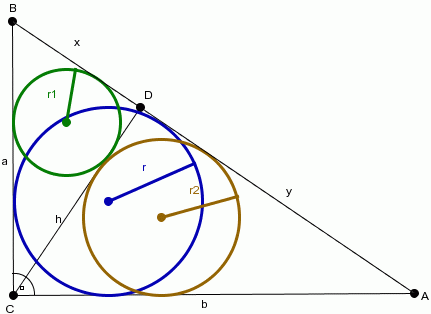
Oznaczam przyprostokątne trójkąta przez a i b, a dwa odcinki powstałe po podzieleniu przeciwprostokątnej przez wysokosc x i y.
W Zadaniu 15 udowodnilismy prawdziwość wzoru: a + b = 2r + c dla trójkąta prostokątnego
gdzie a i b to przyprostokątne, r - promień okręgu wpisanego w trójkąt, a c - przeciwprostokątna trójkąta.
Możemy go wykorzystać:
x + h = b + 2r1
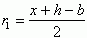
y + h = a + 2r2
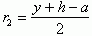
a + b = x + y + 2r
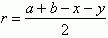
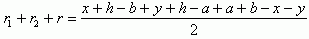
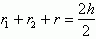
r1 + r2 + r = h
Sposób II:
Tu korzystamy ze wzoru:
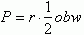 gdzie r jest promieniem okręgu wpisanego
gdzie r jest promieniem okręgu wpisanego
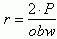
Dla uproszczenia przedstawiamy h, x i y w postaci wyrażeń składających się tylko z wartości a, b i c :
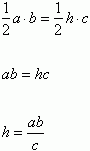
Możemy zauważyć, że trójkąt ABC przystaje do trójkąta DBC, gdyż mają rowne kąty. Wtedy:
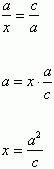
Trójkąt ABC przystaje do trójkąta ACD, więc:
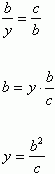
Teraz wyliczamy po kolei wartości dla r, r1 i r2
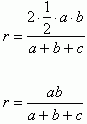
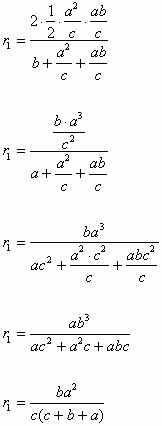
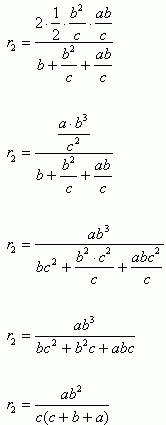
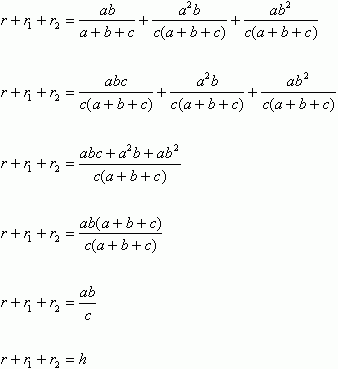
Odpowiedź: Suma promieni okręgów wpisanych w trójkąty: ABC, DBC i ACD są równe wysokości tego trójkąta.
Ania Ługiewicz IIa