LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA PRZYGOTOWAWCZE DO ETAPU III
DLA KLAS II GIMNAZJUM

Zadanie17

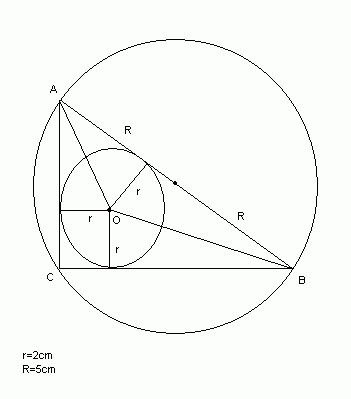
 Wyznacz pole trójkąta prostokątnego, dla którego promień okręgu wpisanego w ten trójkąt równa się 2 cm, a promień okręgu opisanego na tym trójkącie równa się 5 cm.

Rozwiązanie

Dorysowujemy promienie do punktów styczności okręgu wpisanego. Są one prostopadłe do boków i dzielą cały trójkąt na cztery mniejsze trójkąty i kwadrat.

Zauważamy , że dwie pary trójkątów są identyczne (przystające). Trójkąty przystające zaznaczam tymi samymi kolorami:

Niezamalowany kwadrat ma bok długości 2 cm.
Liczymy pole tego kwadratu:

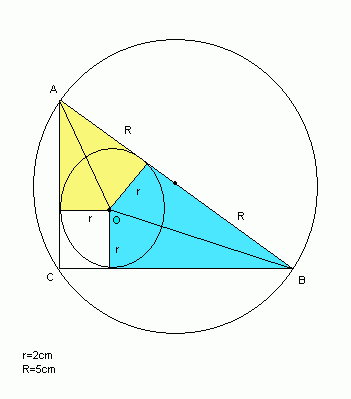
Pk = r2 = 22 = 4 (cm 2)

Teraz zajmijmy się czterema trójkątami. Zauważmy, że suma ich pól jest dwa razy większa niż pole trójkąta (zaznaczonego brązowym kolorem) o podstawie 2R i wysokości r.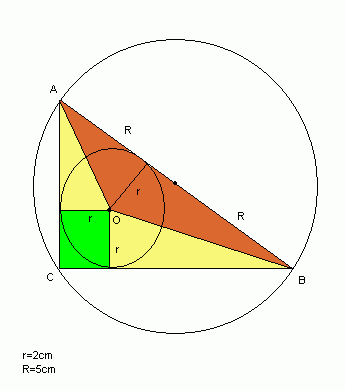

Suma pól tych trójkątów jest więc równa:

Pt = 2 × ½ × 2R ×r = 2R × r = 10 × 2 = 20 (cm2)

Stąd pole dużego trójkąta P = Pt + Pk = 20 + 4 = 24 (cm2)

Odpowiedź:

Pole trójkąta równa się 24 cm 2.

Basia Magrzyk