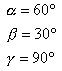LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA WAKACYJNE
DLA UCZNIÓW GIMNAZJUM
Zadanie 19
W trójkącie ABC poprowadzono z wierzchołka C wysokość i środkową. Podzieliły one kąt wewnętrzny przy wierzchołku C na trzy równe kąty. Wyznaczyć kąty trójkąta ABC.Rozwiązanie
Niech S oznacza środek boku AB, a H spodek wysokości wychodzącej z wierzchołka C. Oznaczmy przez g miarę kąta ACB, a przez a miarę kąta BAC. Wtedy a +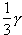
= 90°.
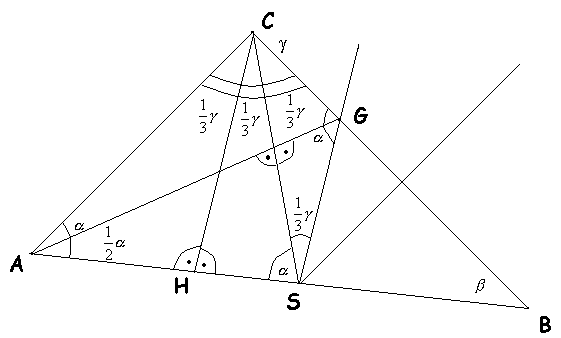
Z warunków zadania wynika, że trójkąt ASC jest równoramienny, bo odcinek CH który jest wysokością trójkąta ABC wyprowadzoną z wierzchołka C jest jednocześnie wysokością trójkąta ASC i dzieli kąt ACS na dwa kąty przystające
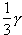( i ).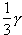
Wynika stąd, że kąt ASC ma też miarę a.
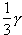Wykonujemy następująca konstrukcję. Kreślimy prostą równoległą do odcinka CH i przechodzącą przez punkt S. Ta prosta przecina odcinek BC w punkcie G. Łatwo jest udowodnić, że kąt GSC jest równy . Wynika to z tego, że kąty GSC i HCS są naprzemianległe.
Z tego, że trójkaty SAC i SGC są równoramienne wynika, że trójkąty ASG i ACG mają boki tej samej długości więc są przystające. Zatem mają takie same kąty.
3 · 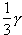= a +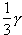
a + 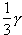= 90°.
g = 90°.
Stąd już łatwo wyliczyć, że a = 60°, b = 30°.Odpowiedź
Paula Mazepa 2a