Liga zadaniowa UMK w Toruniu 2003/2004

Zadanie 19

Uzasadnij, że jeśli n jest liczbą naturalną, to ułamek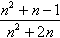

jest nieskracalny?

Rozwiązanie

Należy pokazać, że największy wspólny dzielnik licznika i mianownika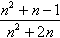 ułamka

jest równy 1.

Niech NWD(n² + n - 1, n² + 2n) = d

Liczby n² + n - 1 i n² + 2n są podzielne przez d, więc ich różnica też jest podzielna przez d:

(n² + 2n) - (n² + n - 1) = n + 1

Liczba n + 1 jest podzielna przez d, a więc jej wielokrotność n(n + 1)również dzieli się przez d:

n(n + 1) = n² + n

Liczby n² + n i n² + n - 1 dzielą się przez d, więc ich różnica też dzieli się przez d.

Ale (n² + n) - (n² + n - 1) = 1, czyli 1 dzieli się przez d.

Wynika stąd, że d = 1, bo jedyną liczbą naturalną, która jest dzielnikiem jedynki jest jedynka.

Jakub Nasierowski