 .
.LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA KONKURSOWE Z ETAPU I
DLA KLAS II GIMNAZJUM
Zadanie 1
Oblicz: 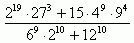 .
.
Rozwiązanie:
Aby obliczyć ten ułamek powinniśmy podstawy potęg, które są liczbami złożonymi zamienić na iloczyn liczb pierwszych:
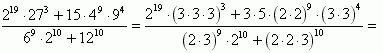
Iloczyny, które znajdują się w nawiasach możemy przedstawić jako iloczyn potęg, gdyż potęga iloczynu równa się iloczynowi potęg. Aby ten ułamek uprościć możemy wykładniki potęg, które mnożymy, dodać do siebie, a ich podstawy przepisać:
=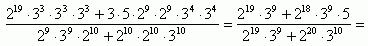
Następnie wynosimy przed nawias potęgi o różnych podstawach i skracamy potęgi o tych samych podstawach, a wyrażenia z nawiasów obliczamy:
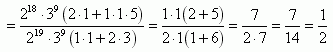
Otrzymujemy wynik 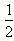 .
.
Odpowiedź:
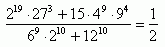
Ewelina Rudnicka