LIGA ZADANIOWA UMK W TORUNIU 2004/2005
ZADANIA KONKURSOWE Z ETAPU II
DLA KLAS II GIMNAZJUM

Zadanie 2

 Na kwadracie ABCD o boku 5 opisano okrąg, a następnie wykreślono okrąg o środku w punkcie A i promieniu AB. Oblicz pole figury zacieniowanej na rysunku obok.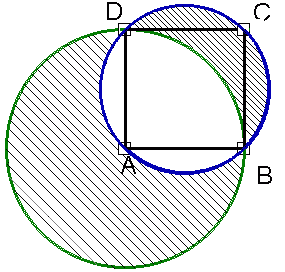

Rozwiązanie

 1. Można zauważyć, że wycinki kołowe X, Y, X' i Y' są przystające (rys.), ponieważ powstały w wyniku opisania okręgu na kwadracie.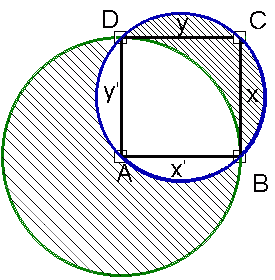
Rozmiar: 5945 bajtów
Przełożywszy więc fragmenty X i Y w miejsce X' Y' otrzymamy ¾ dużego koła (rys2.)
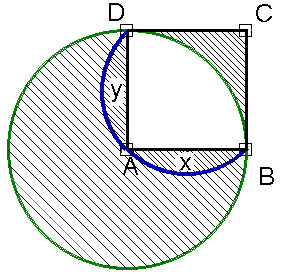Rozmiar: 5559 bajtów
a) obliczamy pole koła:
Pk=p · r2
Pk=p · 52
Pk=25p
b) obliczamy pole zacieniowanej części koła:
P= ¾ · 25p
P= 75/4 p
2.Zauważmy, że figura Z powstaje w wyniku wycięcia z kwadratu ćwiartki dużego koła.

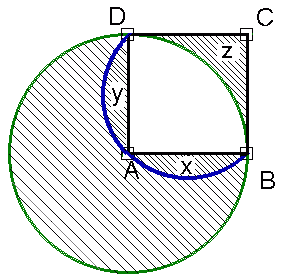Rozmiar: 5593 bajtów
a) obliczamy pole kwadratu:
P=a · a
P=5 · 5
P=25
b) obliczamy pole ćwiartki koła:
P= ¼ · 25p
c) obliczamy pole figury Z:
P=25 - ¼ · 25p
3. Obliczamy pole figury:
P= 75/4 p + 25 - ¼ · 25p
P= 50/4 p + 25 = 25(1 + ½ p)

Odpowiedź

 Pole zacieniowanej figury wynosi 25(1 + ½ p) j2

Hanna Słupska 2a