LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA WAKACYJNE
DLA UCZNIÓW GIMNAZJUM
Zadanie 24
Na okręgu mamy 7 liczb naturalnych. Wiadomo, że w każdej parze sąsiednich liczb jedna z nich jest podzielna przez drugą. Uzasadnić, że istnieją dwie liczby, które nie sąsiadują ze sobą i jedna z nich jest podzielna przez drugą.
Rozwiązanie:
Spróbuję wskazać przykład takiego rozmieszczenia liczb na okręgu, że każdej parze sąsiednich liczb jedna z nich jest podzielna przez drugą,
ale NIE istnieją dwie takie liczby niesąsiadujące, że jedna z nich jest podzielna przez drugą.
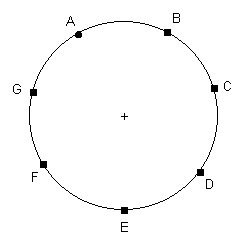
Na następnych rysunkach pomocniczych zwrot
A>B
oznacza, że A jest podzielne przez B.
Załóżmy, że A jest podzielne przez B (a nie B przez A). Gdyby B było podzielne przez C, A także musiałoby być podzielne przez C. Wtedy mieli byśmy przykład liczb nie sąsiadujących ze sobą i podzielnych przez siebie, ale ja próbuję uzasadnić, że takie liczby nie istnieją, więc muszę w takim razie przyjąć, że C jest podzielne przez B (a nie B przez C).
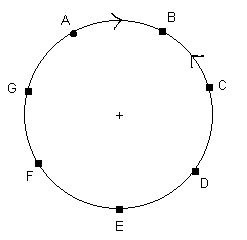
Podobnie rozumując, ustalam co jest podzielne przez co, jak na poniższym rysunku, aż dochodzę do liczby G.
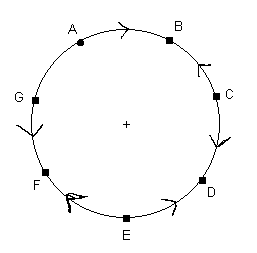
Jeśli G jest podzielne przez A, to jest podzielne także przez B. Jeśli A jest podzielne przez G, to jest podzielne także przez F. Tak więc nie udało się udowodnić, że takie liczby nie istnieją, to znaczy, że istnieją.
Mariusz Szulc



