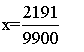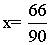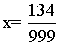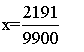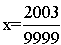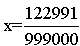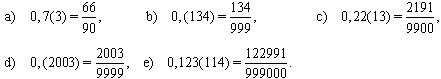LIGA ZADANIOWA UMK W TORUNIU 2003/2004
ZADANIA PRZYGOTOWAWCZE DO ETAPU I
DLA KLAS I GIMNAZJUM
Zadanie 24
Każdy z następujących ułamków przedstaw w postaci ułamka zwykłego:
a) 0,7(3) b) 0,(134) c) 0,22(13) d) 0,(2003) e) 0,123(114)
Rozwiązanie
Przykład a)
0,7(3)oznaczamy jako x
x = 0,7(3)
x = 0,73333..... / 100 (obydwie strony równania mnożymy przez 100)
100x = 73,3333....
- 10x = 7,33333 (od 100x odejmujemy 10x aby pozbyć się częśći ułamka, po przecinku.)
90x = 73,3333... - 7,3333 = 66
90x = 66 /: 90 (obie strony dzielimy przez 90)
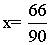
Przykład b)
0,(134) oznaczamy jako x
x = 0,(134)
x = 0,134134134..... / 1000 (obie strony równania mnożymy przez 1000)
1000x = 134,134134....
- x = 0,134134..... (od 1000x odejmujemy x aby pozbyć się częśći ułamka, po przecinku.)
999x = 134,134134.... - 0,134134.... = 134
999x = 134 / : 999 (obie strony dzielimy przez 999)
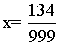
Przykład c)
0,22(13) oznaczamy jako x
x = 0,22(13)
x = 0,221313131313..... / 10000 (obie strony równania mnożymy przez 10000)
10000x = 2213,131313....
- 100x = 22,131313.... (od 1000x odejmujemy 100x aby pozbyć się częśći ułamka, po przecinku.)
9900x = 2213,131313.... - 22,131313.... = 2191
9900x = 2191 / : (obie strony dzielimy przez 9900)